Rychlý průnik množin a Jaccardův index přes SIMD instrukce
Na funkcionálně.cz jsem kdysi psal, jak rychle počítat Jaccardův index podobnosti. Jaccard udává míru, do jaké jsou si dvě množiny podobné jako velikost průniku vydělenou velikostí sjednocení. Ke své práci potřebuje co nejrychleji spočítat velikost průniku a to jsem v článku rozebíral. Od triviálních pokusů jsem se propracoval k množinám ve formě seřazených polí, vektorizované verzi, minhashování a LSH.
Něco na ten způsob jsem zase potřeboval a proto je čas téma oprášit ještě jednou a naposledy.
Intel do x86 v rozšíření SSE 4.2 přidal pár instrukcí zamýšlených pro
zrychlení práce se stringy (tak jsou použity např. v JVM). Umí toho
ale mnohem víc. Jedna z nich – velice mocná operace pcmpestrm – se dá využít
pro rychlý výpočet průnik množin.
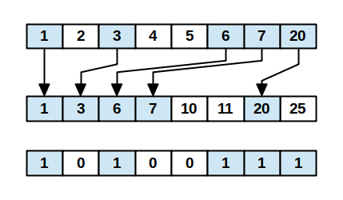
Jedna varianta pcmpestrm vezme dva 128bitové registry, obsah interpretuje
jako pole osmi 16b intů a vyprodukuje bitmasku udávající, které hodnoty z prvního registru se vyskytují někde v tom dalším. Neporovnává dva vektory
paralelně, první element s prvním, druhý s druhým a tak dál, ale každý element
se každým najednou. Jedna instrukce tak provede 64 porovnání a další verze,
která vstupy bere jako šestnáct 8b intů, vykoná rovnou 256 porovnání. A přesně
tohle potřebujeme.
Skalární verze velikosti průniku (v jazyku D) vypadá takhle:
int intersectionSize(T)(T[] a, T[] b) { int ai, bi, count; for (; ai < a.length && bi < b.length; ) { T aa = a[ai]; T bb = b[bi]; count += (aa == bb); ai += (aa <= bb); bi += (aa >= bb); } return count; }
Vezme dva elementy, porovná je, když jsou stejné, inkrementuje počet a oba indexy, jinak posune index ukazující na menší z nich o jedno místo dopředu. Jde o velice jednoduchý kód, bez podmíněných skoků ve smyčce a tak branch predictor nemůže být zmaten z nepředvídatelných vstupů.
Vektorová verze z tohoto paperu (pozor, v ukázce kódu mají chybu) funguje na stejném principu, pracuje jen s celými vektory najednou, namísto jednotlivých elementů.
while (ai < a.length-7 && bi < b.length-7) { ushort8 av = cast(ushort8) __builtin_ia32_loaddqu(cast(char*)&a.ptr[ai]); ushort8 bv = cast(ushort8) __builtin_ia32_loaddqu(cast(char*)&b.ptr[bi]); int4 res = cast(int4) __builtin_ia32_pcmpestrm128( cast(ubyte16)bv, 8, cast(ubyte16)av, 8, 0x01 // _SIDD_UWORD_OPS | _SIDD_CMP_EQUAL_ANY | _SIDD_BIT_MASK ); ushort a7 = av.array[7]; ushort b7 = bv.array[7]; ai += (a7 <= b7) * 8; bi += (a7 >= b7) * 8; count += popcnt(res.array[0]); }
Kód je ošklivý a matoucí, jak bývá při použití intrinsics funkcí, funguje
jen pro 2B elementy (pcmpestrm přímo nepodporuje vektory 4B intů, ale existují
jiná řešení), ale jede rychle a jen na tom záleží. Výsledky v jedné úloze,
která počítá Jaccarda pro velký počet množin, jsou tyto:
| skalární průnik | 170.6 s |
| SSE + skalární | 113.6 s |
| pouze SSE | 78.1 s |
Druhý řádek je v podstatě úryvek kódu výše zpracovávající bloky osmi 16 intů a po něm běží skalární verze, která dojede zbytek. Při profilování se ukázalo, že
právě tam program tráví zbytečně dlouho. Třetí řádek v tabulce představuje
plně SSE verzi (zdroják tady), která všechno řeší přes pcmpestrm a rychlostí značně vyčnívá.
Ve výsledku je možné (v tomto případě a na tomto stroji) dosáhnout víc než dvojnásobného zrychlení jenom tím, že využijeme všechny možnosti hardwaru. Navíc nejde o nic extra, SSE 4.2 Intel uvedl víc jak před dekádou a proto se můžeme spolehnout, že bude na každém procesoru, kde program poběží.
Dodatek: Jiný program za použití téhle metody zrychlil asi 4.2×.